この記事は
・固体物理を勉強中
・バンドギャップの原因が知りたい
・金属や半導体、絶縁体の違いは何か知りたい
といった方向けに書きました。
理系大学生や、文学を読むのが好きな方のために、こちらのページで無料で多数の本が読めるリンクをまとめています。非常に有益ですので是非お読みください。
以下の本を参考にさせていただきました。
まとめ
用語
とりあえず主要用語の説明をします。
エネルギーバンド:結晶中において、電子が存在するエネルギー領域
バンドギャップ:結晶中において、電子が存在できないエネルギー領域
バンドギャップエネルギー:バンドギャップのエネルギー差。マクロな量。
結論
結論としては以下の通りです。
絶縁体や半導体、金属の違いの原因は、その物体中の電子のバンドギャップ、およびバンドギャップエネルギーの大きさにあります。
バンドギャップの原因は、結晶中の電子のポテンシャルエネルギーが周期的なポテンシャルエネルギーであることです。
以下でこのことを見ていきます。
周期ポテンシャルがバンドギャップを作るのを見るために、ポテンシャルが0の自由電子モデルと、ポテンシャルが周期的なクローニッヒ-ペニーモデルを比較してみます。
その後で絶縁体や半導体、金属の違いをグラフで見てみることにします。
ただし、以下全て1次元格子とします。また、格子定数はaです。
自由電子モデル
このモデルは、ポテンシャルエネルギーが0というのが特徴です。
つまり、シュレーディンガー方程式としては、電子の質量をmとして
$$-\frac{\hbar^{2}} {2m} \frac{d^2}{dx^2}\psi(x) = E \psi(x)$$
と書けます。
これを周期境界条件
$$\psi (x+a)=\psi (x)$$
の下で解くと
$$E_{k} =\frac{\hbar^2 k^2}{2m}$$
$$k=\frac{2n\pi}{a} \qquad (nは整数)$$
$$\psi_{k}(x)=Ae^{ikx} \qquad (Aは定数)$$
と導くことができます。今回はこれが本題ではないので導出はスキップしました。
さて、ここでエネルギーと波数の関係式があることが分かります。
また、波数は第二式のように離散的な値をとりますが、マクロに見れば連続的に見えるので、連続変数と見なすことができます。
したがって、第一式をグラフに書くと以下のようになります。
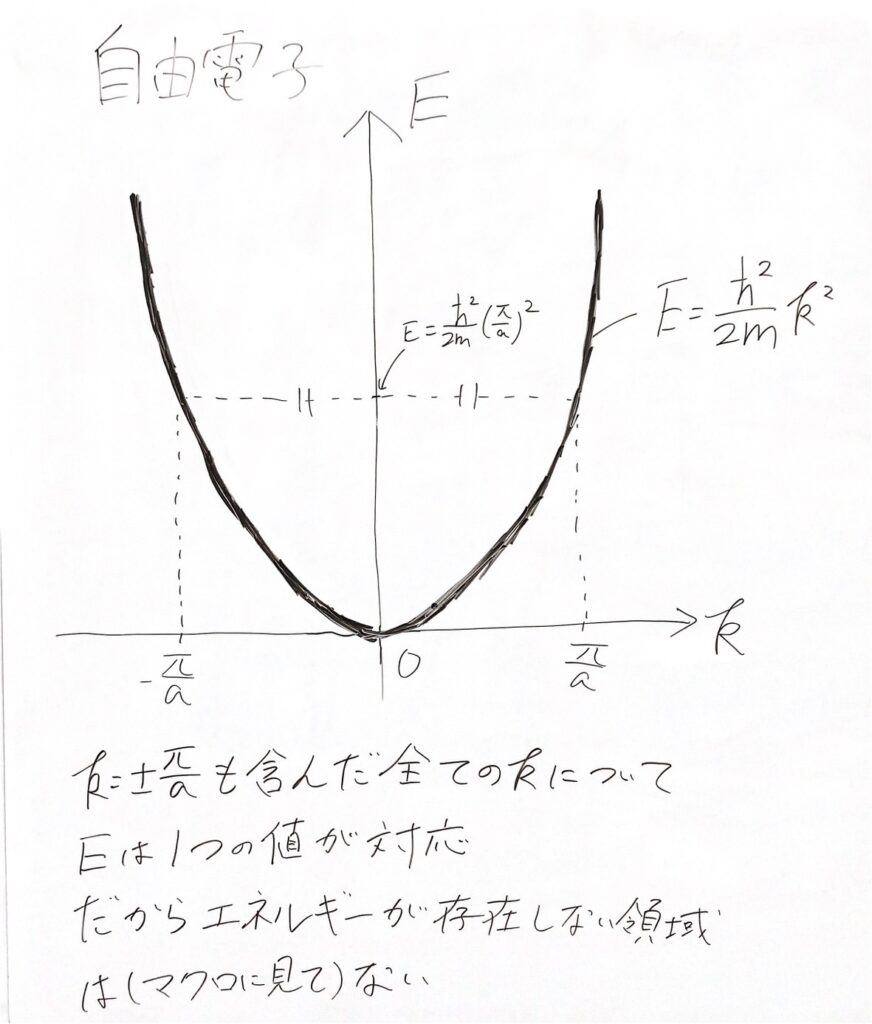
これを見ると、特に電子に対して制約がない、つまり自由電子モデルの場合は「電子が存在できないエネルギー領域」がないことが分かります。
このグラフが重要です。後でまた取り上げます。
クロ―ニッヒ-ペニーモデル
このモデルを一言で言うと、「シュレーディンガー方程式でのポテンシャルを周期ポテンシャルに変えた時に、バンドギャップとエネルギーバンドが発生するのを示すためのモデル」です。
自由電子モデルでは、電子のポテンシャルを0としました。
このモデルでは、電子のポテンシャルを「周期ポテンシャル」として導入します。
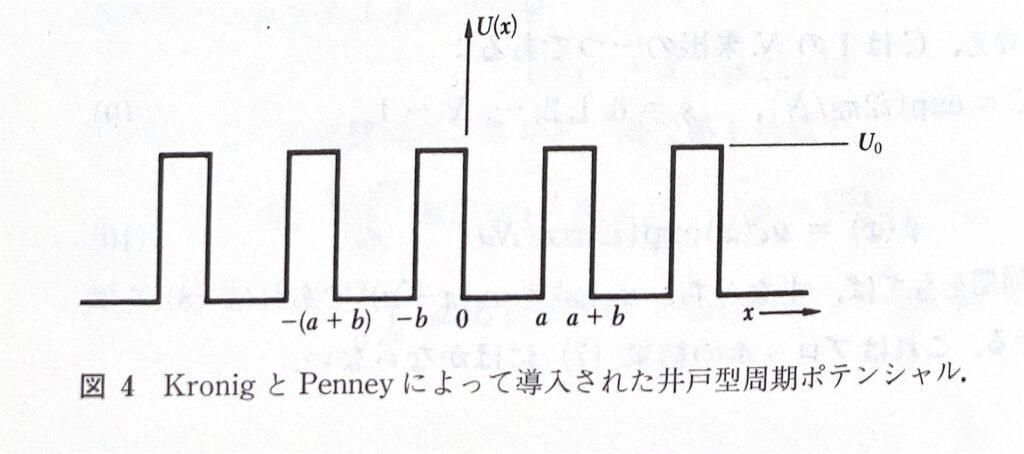
このモデルで使う周期ポテンシャルは以下のポテンシャルになります。
『キッテル 固体物理学入門(上)』7章 178ページより引用
計算
これより、シュレーディンガー方程式は以下のようになります。
$$-\frac{\hbar^{2}} {2m} \frac{d^2}{dx^2}\psi(x) = E \psi(x) \qquad (0<x<a)$$
$$-\frac{\hbar^{2}} {2m} \frac{d^2}{dx^2}\psi(x)+U_{0}\psi(x) = E \psi(x) \qquad (-b<x<0)$$
これらを解くと
$$\psi_{1}(x)=Ae^{iKx}+Be^{-iKx} \quad,\quad K=\frac{\sqrt{2mE}}{\hbar} \qquad (0<x<a)$$
$$\psi_{2}(x)=Ce^{Qx}+De^{-Qx}\quad ,\quad Q=\frac{\sqrt{2m(U_{0}-E)}}{\hbar} \qquad (-b<x<0)$$
となります。
定数A~Dは次の条件
$$\psi_{1}(0)=\psi_{2}(0)$$
$$\frac{d\psi_{1}}{dx}(x=0)=\frac{d\psi_{2}}{dx}(x=0)$$
とブロッホの定理を組み合わせた
$$\psi_{1}(a)=\psi_{2}(a) \times exp[ik(a+b)]$$
$$\frac{d\psi_{1}}{dx}(x=a)=\frac{d\psi_{2}}{dx}(x=a) \times exp[ik(a+b)]$$
の4つの式から求めることができます。
補足 ブロッホの定理
周期ポテンシャル中のシュレーディンガー方程式の解(つまり波動関数)の形は
$$\psi(\boldsymbol{r})=u(\boldsymbol{r})e^{i \boldsymbol{k}\cdot \boldsymbol{r}} $$
$$u(\boldsymbol{r}+\boldsymbol{R})=u(\boldsymbol{r}) \quad, \quad \boldsymbol{R}=(並進ベクトル)$$
で表せることが知られています。
この定理をブロッホの定理と呼び、この波動関数をブロッホ関数と言います。
今回使ったのは一次元でのブロッホの定理で、
$$\psi(x)=u(x)e^{ikx}$$に周期Tを適用した
$$\begin{eqnarray} \psi(x+T)=u(x+T)e^{ik(x+T)}\\=u(x)e^{ikx}e^{ikT} =\psi(x)e^{ikT} \end{eqnarray}$$
です。これにx=-b、T=a+bを(微分などしてから)代入すると上のブロッホの定理を用いた二つの条件式が導けます。
これにΨを代入すると以下の式が求まります。
$$A+B=C+D$$
$$iK(A-B)=Q(C-D)$$
$$Ae^{iKa}+Be^{-iKa}=(Ce^{-Qb}+De^{Qb})exp[ik(a+b)]$$
$$iK(Ae^{iKa}-Be^{-iKa})=Q(Ce^{-Qb}-De^{Qb})exp[ik(a+b)]$$
※大文字のKと小文字のkが分かりにくいと思うので、小文字の方はexpで表しています。
これらは、A~Dの4つの係数が作る行列式の値が0の時にのみ解をもちます。以下の行列式の手計算の画像を張っておきます(タイプ入力だと大変なので手書きにしました)。

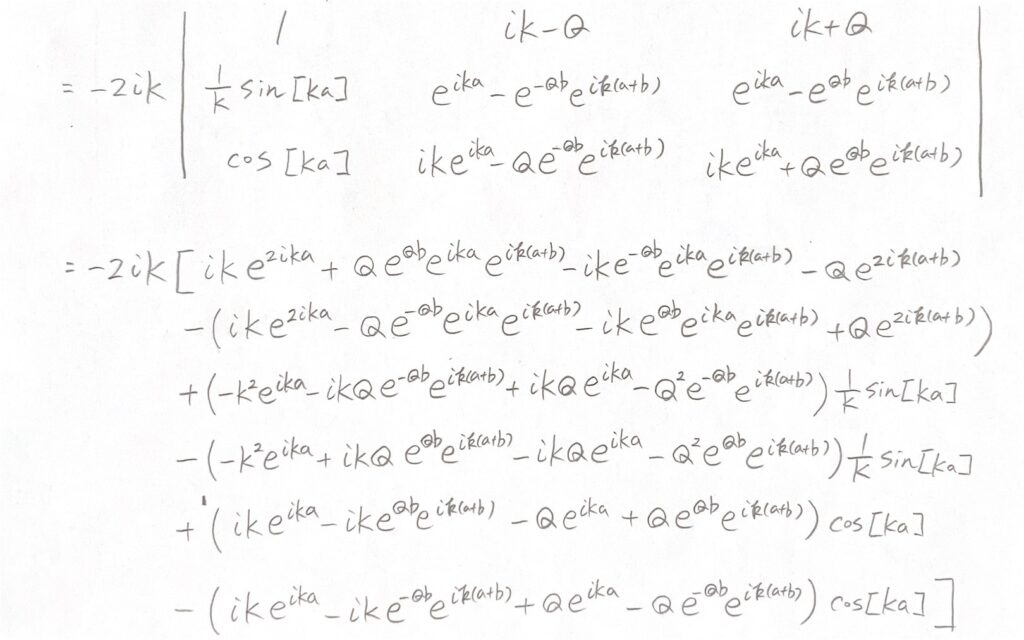
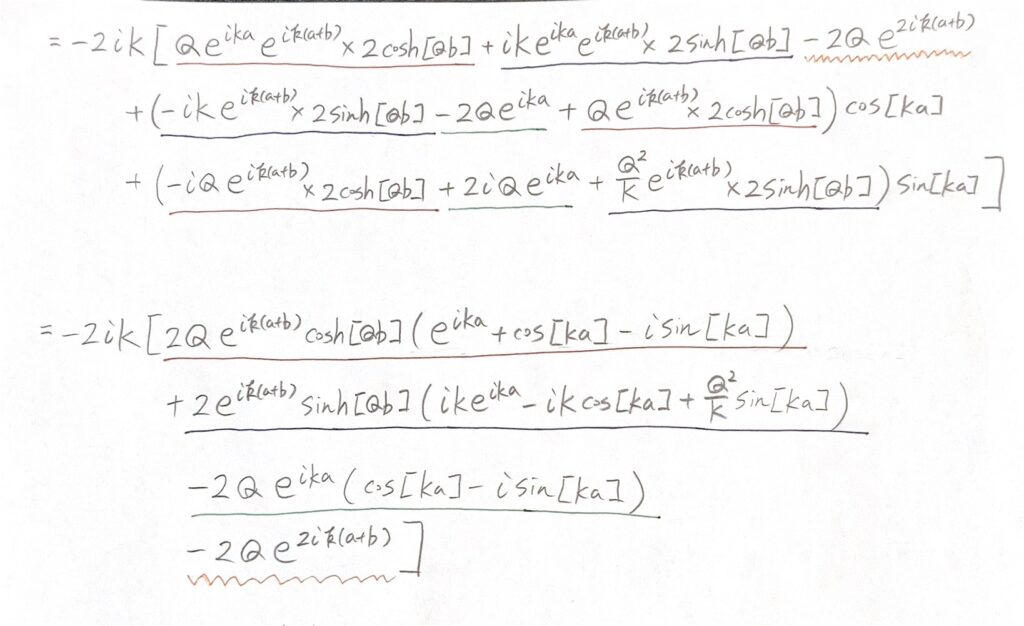
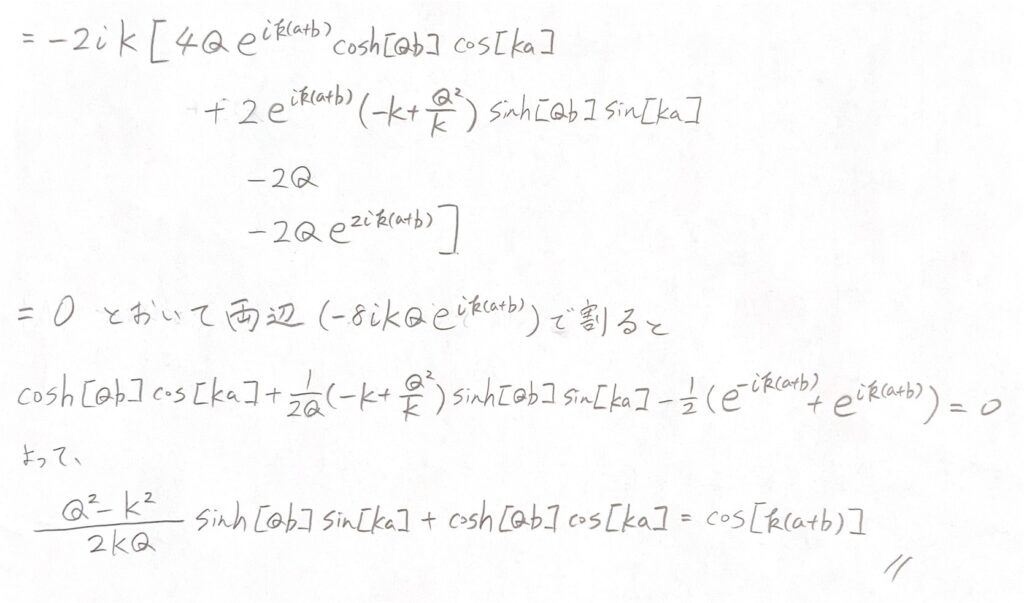
よって、
$$\frac{Q^2 – K^2}{2QK}sinh[Qb]sin[Ka]+cosh[Qb]cos[Ka]=cos[k(a+b)]$$
という式を得ます。
近似
でも、このままだと非常に分かりにくいので近似を使います。
具体的には、b→0の極限において、$$P=\frac{Q^2 ab}{2}$$が有限値を持つように$$Q>>K \quad , \quad Qb<<1$$とします。
ここでx<<1のとき
$$sinh[x] \approx x$$
$$cosh[x] \approx 1$$
を使います。すると、
$$\begin{eqnarray} \frac{Q^2 – K^2}{2QK}sinh[Qb]sin[Ka] \approx \frac{Q^2}{2QK}\times Qb \times sin[Ka] \\=\frac{P}{QbKa} \times Qb \times sin[Ka] =\frac{P}{Ka} sin[Ka] \end{eqnarray}$$
と第一項が近似でき、第二項は簡単で
$$cosh[Qb]cos[Ka] \approx 1\times cos[Ka] = cos[Ka]$$
と近似できます。右辺についてはb=0とすればよいので
$$(右辺)=cos[k(a+b)]=cos[ka]$$
となります。Kとkが紛らわしいので$$\theta=Ka$$と置くと
$$\frac{P}{\theta} sin[\theta]+cos[\theta]=cos[ka]$$
という式が出てきたことになります。
近似式をグラフ化
この近似式をグラフとして表すと以下のようになります。
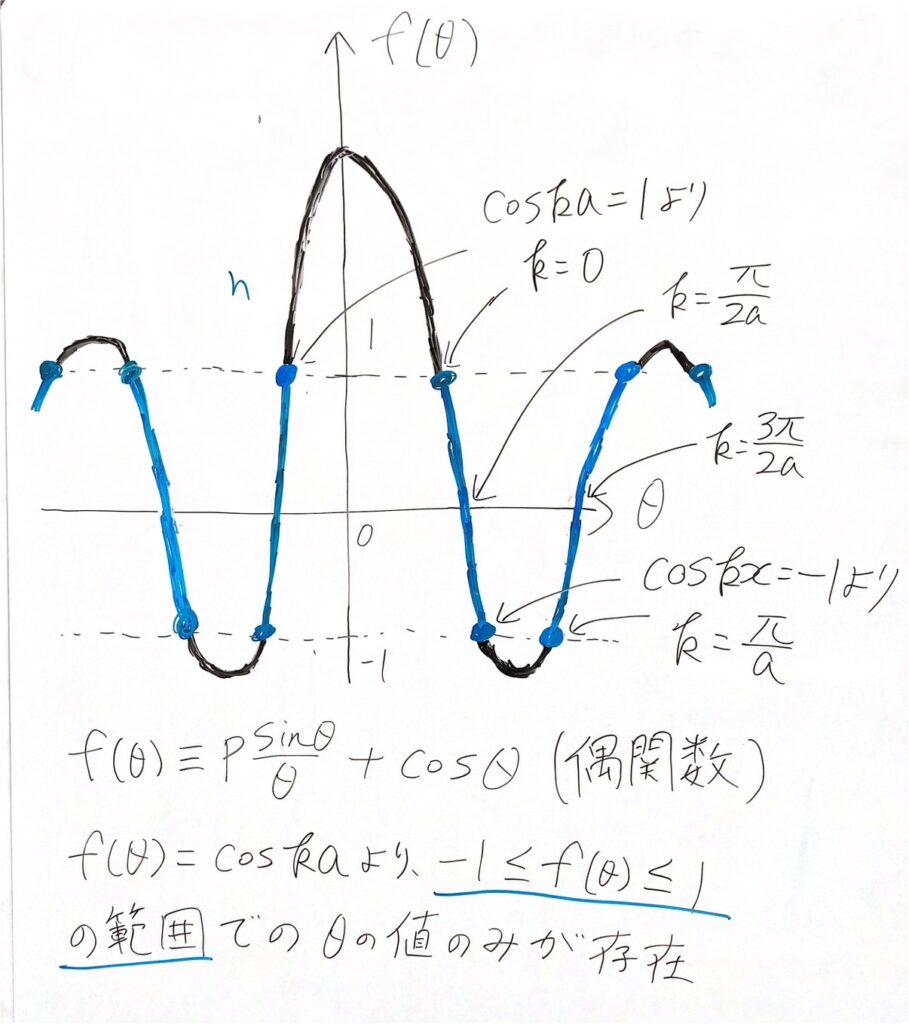
このグラフで注目してほしいのが、$$k=\frac{n\pi}{a} \quad (nは整数)$$の一つの波数の値に対して、θは異なる2つの値が対応していることです。他のkの値についてはθが一つ対応しています。
$$\theta=Ka=\frac{\sqrt{2mE}}{\hbar}a$$
よりθはEとの関係を持ち、したがって$$k=\frac{n\pi}{a}$$という一つの(特殊な)波数に対して2つの異なるエネルギーの値が与えられていることになります。
バンドギャップを図示
これがまさにバンドギャップです。これを図示するとこうなります。
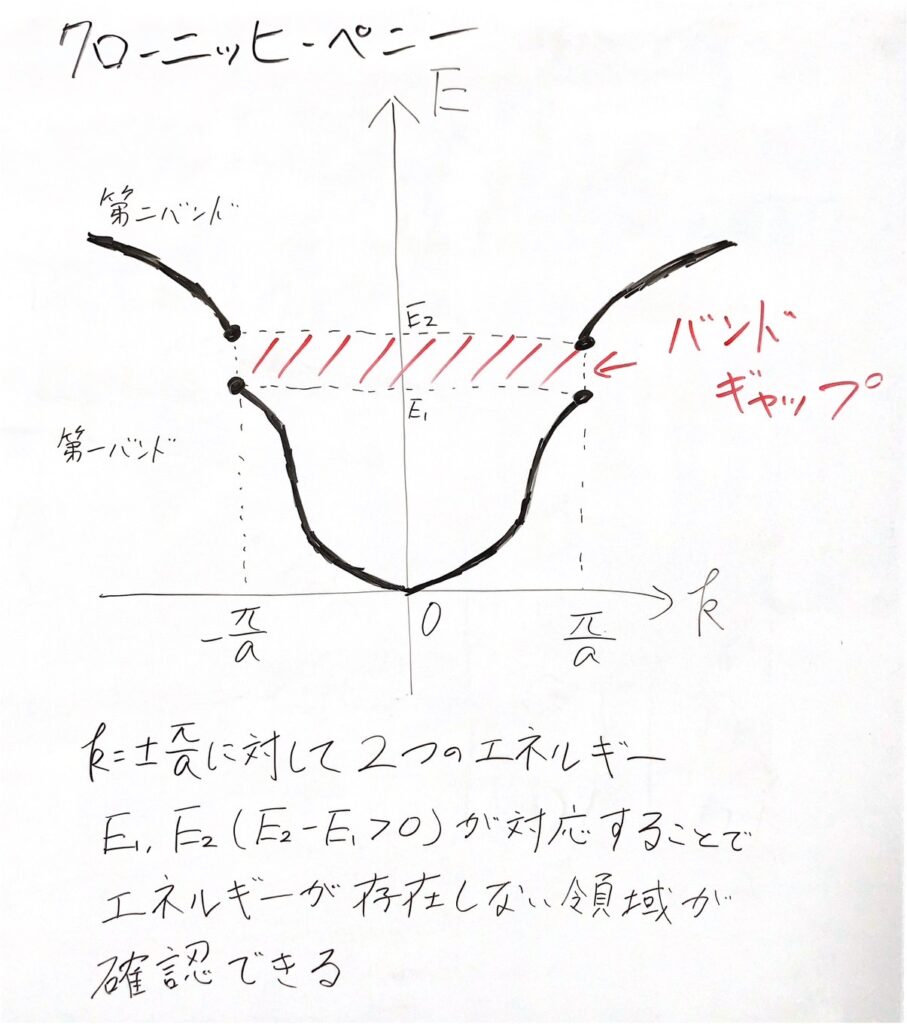
最初のバンド帯(第一バンド)が$$-\frac{\pi}{a} \leq k \leq \frac{\pi}{a}$$にあるので、この区間を第一ブリルアンゾーンと言います。
第二バンド帯は$$-\frac{2\pi}{a} \leq k \leq -\frac{\pi}{a}$$と$$\frac{\pi}{a} \leq k \leq \frac{2\pi}{a}$$の二つの領域で、第二ブリルアンゾーンと言います。
これと自由電子モデルのエネルギーと波数の分散関係を比べてみましょう。
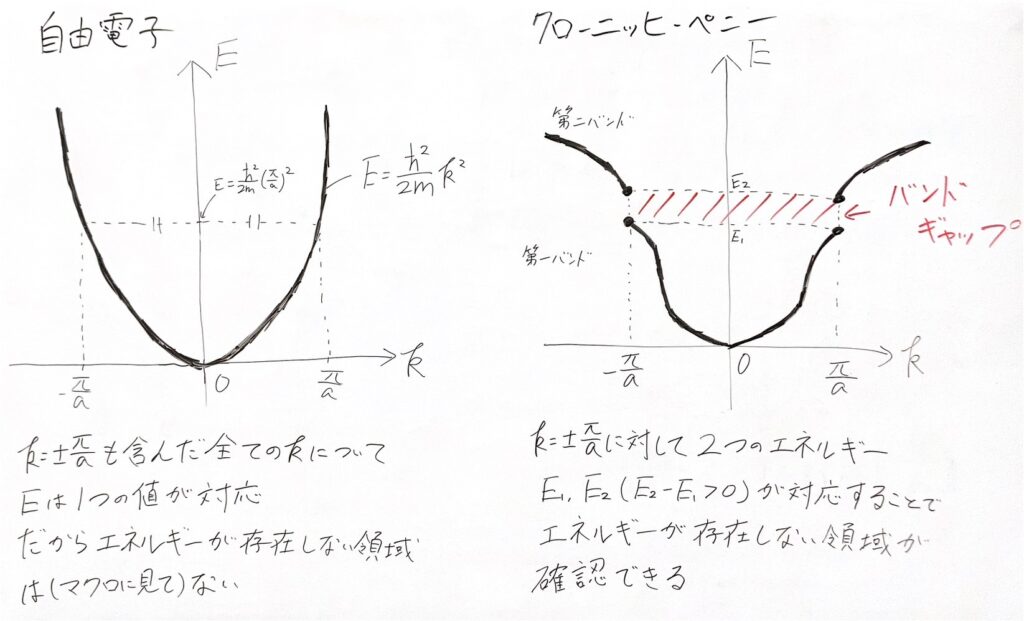
このように、自由電子モデルでは連続だったのに、ペニーモデルでは不連続になっていること(つまりバンドギャップが存在すること)が一目瞭然です。
以上で、バンドギャップは周期ポテンシャルによって発生することが分かったと思います。
絶縁体、半導体、金属
用語
再度載せてあるのもあります。以下の説明で用いる言葉です。
エネルギーバンド:結晶中において、電子が存在するエネルギー領域
バンドギャップ:結晶中において、電子が存在できないエネルギー領域
価電子帯:エネルギーの低いエネルギーバンド
伝導帯:エネルギーの高いエネルギーバンド
バンドギャップエネルギー:伝導帯の底のエネルギーと価電子帯の頂点のエネルギーの差
励起:光子などからエネルギーを受けた電子が、価電子帯から伝導帯にジャンプする現象。バンドギャップエネルギーが大きいと励起しにくい。
違いについて
これらを分けるのはバンドギャップです。図にするとすぐに分かります。
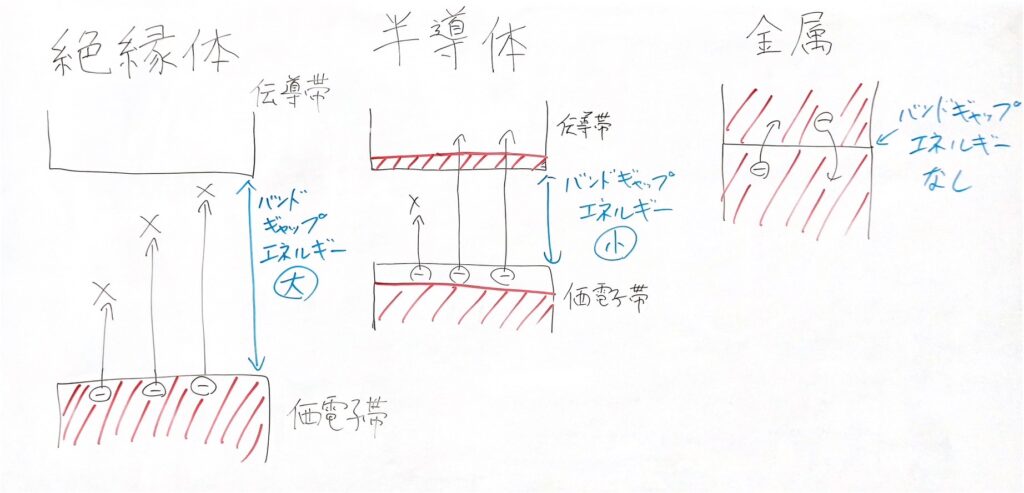
これを用いて説明していきます。
絶縁体
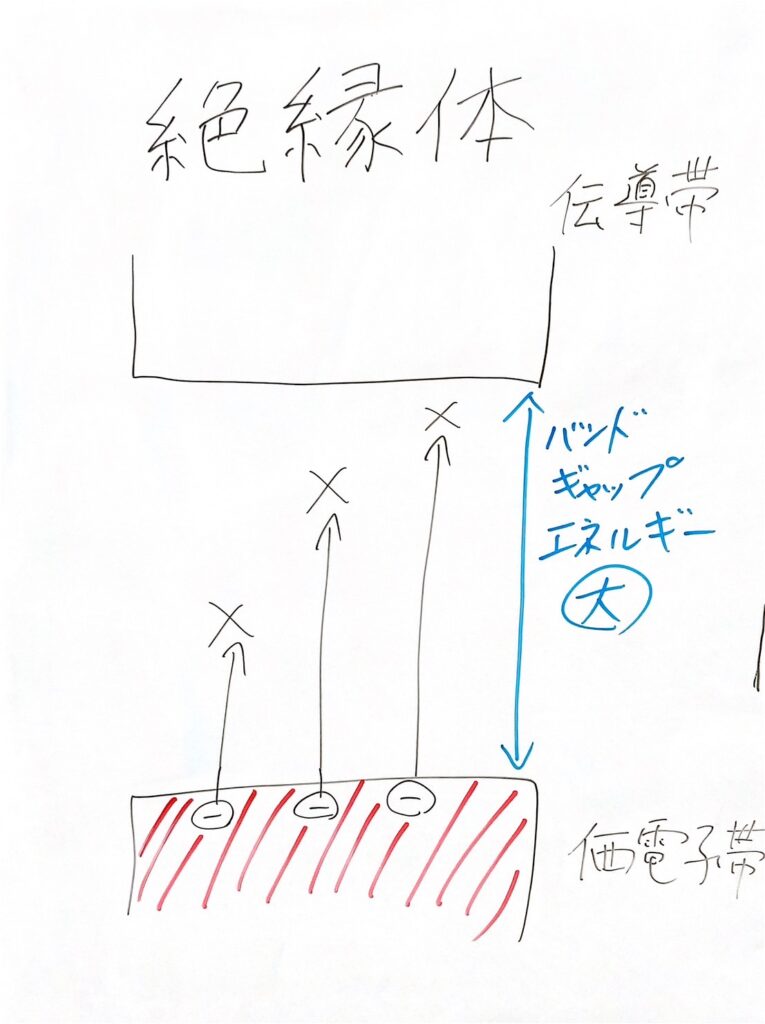
絶縁体の特徴はエネルギーギャップが存在し、そのエネルギーギャップエネルギーが大きいことです。
エネルギーギャップエネルギーが大きいので、電子がちょっとやそっとじゃ励起できません。
したがって価電子帯が(ほとんど)全て電子で埋まっている状態で、伝導帯には電子が移らず、電子は束縛されています。
電流としての役割を果たす自由な電子は全くありません。だから電流が流れません。
例えば2つの電車がある駅に停まっていて、あなたが片方に乗っているとします。あなたが乗っているのは満員電車で、あなたの前にはプラットフォームを挟んで誰も乗っていない空の電車があります。プラットフォームに足をつけないで、ジャンプで10メートル先の空の電車に乗り移れるでしょうか?無理です。
絶縁体の場合はこの電車の間のプラットフォームの幅が広いので、誰も向こうの電車まで行けません。そしてあなたは満員電車の中にいなければならず、束縛されています。
金属
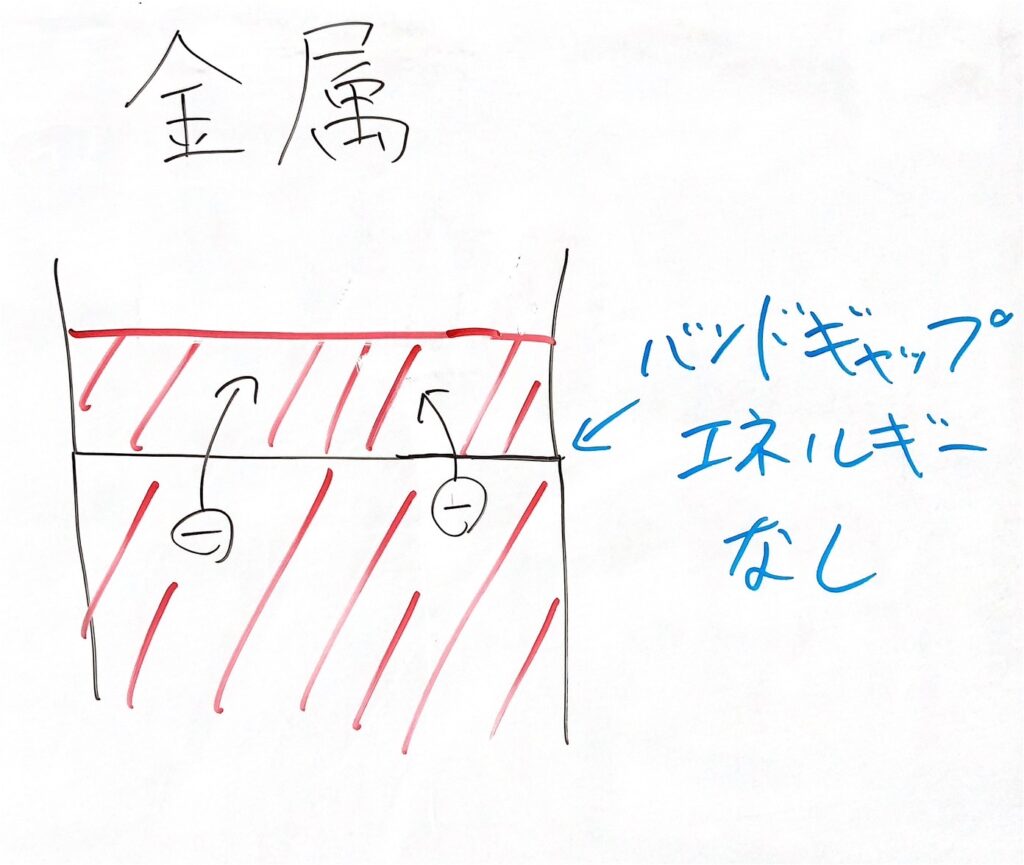
金属の特徴は、エネルギーギャップがそもそもないことです。
だから電子が価電子帯から伝導体へ移ることができます。それにより、束縛から解放された電子によって電流が流れます。
先ほどの例を持ち出せば、2つの電車の入り口はぴったりくっついていて、乗り降り自由です。
半導体
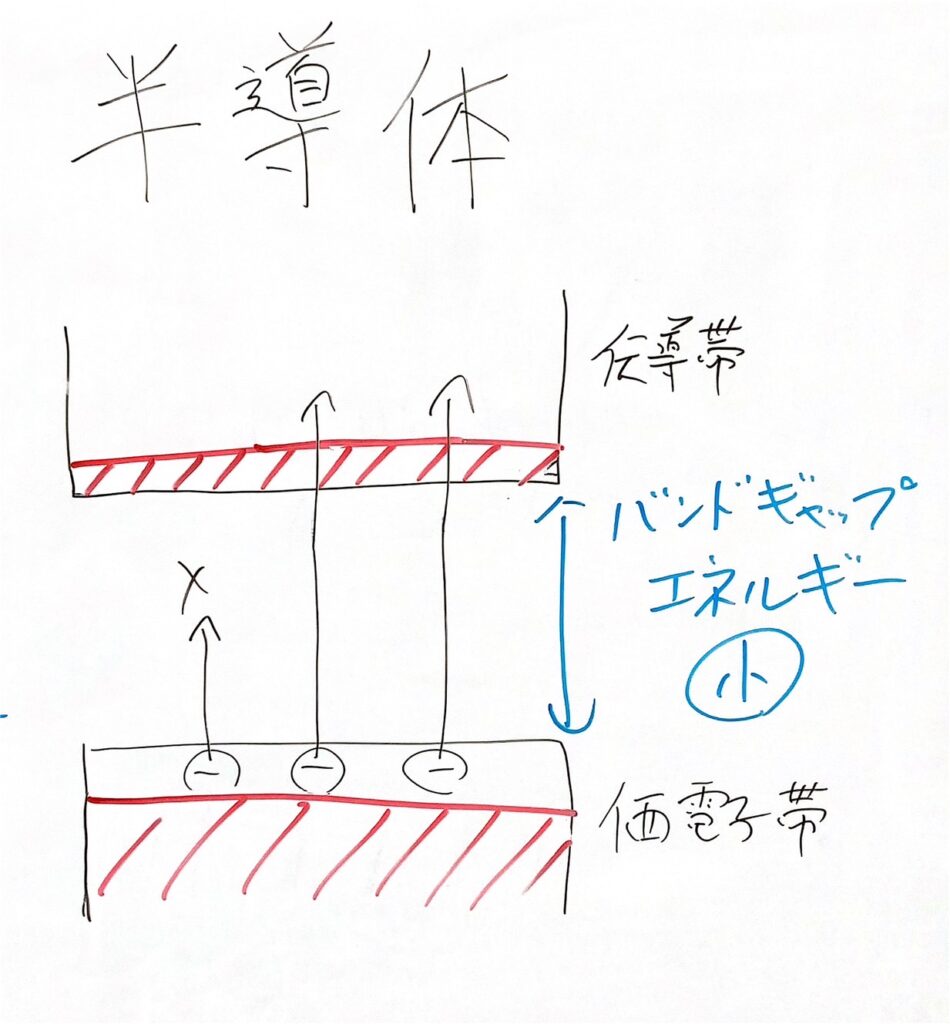
半導体はその名前の通り、金属と絶縁体の中間の性質を持ちます。
簡単に言うと、エネルギーギャップは存在(=絶縁体の性質)しますが、電子が励起できるくらいエネルギーギャップが小さい(=電流として振る舞う電子が存在する=金属の性質)のが半導体です。
先ほどの例だと、プラットフォームはあるけど、これが大体2メートルくらい。全員とはいきませんが、ジャンプが得意な人ならこれくらいの距離なら飛び越えて空の電車に飛び移れるでしょう。で、飛び移った人たちはそこまで多くないのに、広大なスペースが与えられるので自由に動けるというわけです。
理系大学生や、文学を読むのが好きな方のために、こちらのページで無料で多数の本が読めるリンクをまとめています。非常に有益ですので是非お読みください。