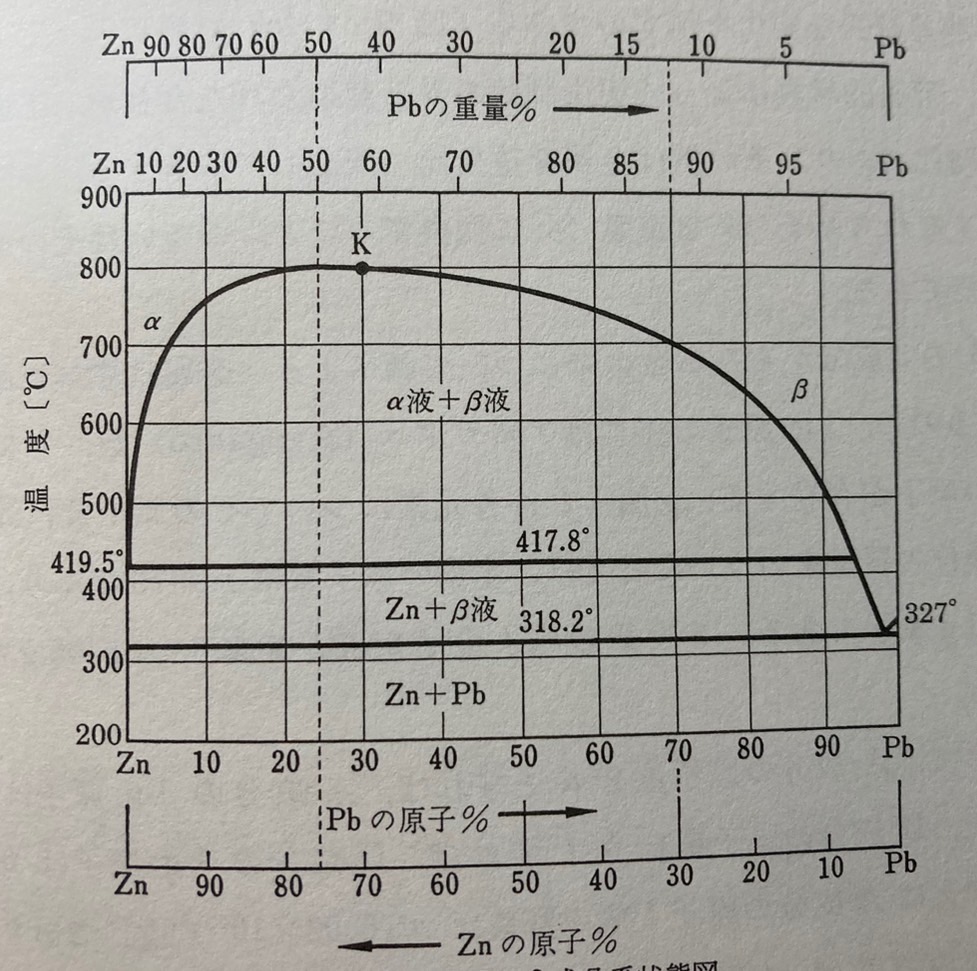
今回の疑問
原子%と重量%の変換はどうすれば良いのか?
引用元 『図解合金状態図読本』 (横山 享) 4章
この画像の上下のように、2成分状態図を見る際には、重量%と原子%の2種類の組成があります。今回はこれらの変換式を見ていきます。
重量%とは?
重量%とは、成分の質量の割合を指します。
成分Aの質量がa(g)、成分Bの質量がb(g)、合金の質量がm(=a+b)(g)だとすると
$$(成分A):(成分B)=a:b=\frac{a}{m}\times 100:\frac{b}{m}\times 100$$
になります。
原子%とは?
原子%とは、成分の原子数の割合を指します。
原子数とは?
原子数とは文字通り、原子の個数のことです。物体は原子から構成されています。そして元素によって(つまりHとかCとかの種類によって)原子1つ当たりの質量が違います。違う言い方をすると、元素によって、同じ質量に含まれる原子の数が異なるのです。だから元素によって原子数が異なります。
成分Aの原子数をA(個)、成分Bの原子数をB(個)、合金の原子数をM(=A+B)(個)だとすると
$$(成分A):(成分B)=A:B=\frac{A}{M} \times 100:\frac{B}{M}\times 100$$
になります。
重量%から原子%に換算
前提
まずは、重量%が分かっている状態で、それを原子%に変換します。
上記の定義を見てみると、原子%を求めるためには、成分AとBの原子数をそれぞれ求めればよいことが分かります。設定としては以下のようにします。合金の質量はM (g)とします。

原子量とは?
原子量(g/mol)とは、原子1molあたりの質量を表します。言い換えると、\(6.0\times 10^{23}\)個の原子の総重量を表します。原子量の逆数(mol/g)は、原子1gあたりの原子の個数を表します。
アボガドロ数とは?molとは?
アボガドロ数とは、1molあたりの原子の数を表し、
$$N=6.0\times 10^{23} (個/mol)$$
と表されます(本当の単位は(/mol))。つまり、molとは\(6.0\times 10^{23}\)個の粒子をひとまとまりにした単位ということです。1ダース=12本と同じことです。
では求めていきます。
原子%を求める
原子量の逆数は、原子1gあたりの原子数を表すのでしたね。具体的には、成分A、Bそれぞれの1gあたりの原子数は
$$\frac{1}{a} (mol/g) \times 6.0\times 10^{23} (個/mol) =\frac{6.0\times 10^{23}}{a} (個/g)$$
$$\frac{1}{b} (mol/g) \times 6.0\times10^{23} (個/mol) =\frac{6.0\times 10^{23}}{b} (個/g)$$
ということになります。
これに成分Aの質量を、質量%から求めて、上で求めた1gあたりの原子数にかければ成分Aの原子数が求まりますね。
$$\begin{eqnarray} (成分Aの質量)=M (g) \times \frac{x}{100}\\=\frac{Mx}{100} (g) \end{eqnarray}$$
$$\begin{eqnarray} (成分Bの質量)=M (g) \times \frac{100-x}{100}\\=\frac{M(100-x)}{100} (g) \end{eqnarray}$$
よって、原子数は
$$\begin{eqnarray} (成分Aの原子数)=\frac{Mx}{100} (g) \times \frac{6.0*10^{23}}{a} (個/g)\\=\frac{6.0\times 10^{23}Mx}{100a} (個) \end{eqnarray}$$
$$\begin{eqnarray} (成分Bの原子数)=\frac{M(100-x)}{100} (g) \times \frac{6.0*10^{23}}{b} (個/g)\\=\frac{6.0\times 10^{23} M(100-x)}{100b} (個) \end{eqnarray}$$
これより、全体としての原子数は
$$\begin{eqnarray} (全体の原子数)=\frac{6.0\times 10^{23}Mx}{100a} (個)+\frac{6.0\times 10^{23} M(100-x)}{100b} (個)\\=\frac{6.0\times 10^{23} M[bx+a(100-x)]}{100ab} (個) \end{eqnarray}$$
したがって、原子%は
$$ (成分A)=\frac{(成分Aの原子数)}{(全体の原子数)}\quad \times 100=\frac{100bx}{a(100-x)+bx}$$
$$(成分B)=\frac{(成分Bの原子数)}{(全体の原子数)}\quad \times 100=\frac{100a(100-x)}{a(100-x)+bx} $$
これで重量%から原子%を求めることが出来ました。
参考文献
『図解合金状態図読本』 (横山 享)